Problemreduktion – Der sicherste Weg ist auch nur ein kürzester Weg

3 Antworten

Anwendungen wie Google Maps oder Navigationssysteme berechnen ständig kürzeste oder auch schnellste Wege. Es gibt bereits seit den 50er Jahren sehr effiziente Algorithmen, um diese Aufgabe zu lösen. Der zuverlässigste Weg kann durch die gleichen Verfahren gefunden werden – mit Hilfe eines kleinen Tricks.

In den 50er und 60er Jahren wurden mehrere Algorithmen zur Lösung des Kürzeste-Wege-Problems erfunden. Darunter waren der Dijkstra-Algorithmus, der Bellman-Ford-Algorithmus und einige Jahre später der A*-Algorithmus. Diese Algorithmen sind zwar für leicht unterschiedliche Einsatzgebiete optimiert, aber sie lösen im Prinzip alle das gleiche Problem: Sie berechnen, auf effiziente Art und Weise, die kürzesten Wege in einem Straßennetz, oder (wie man es in der Informatik betrachtet) in einem Graphen mit Knoten und Kanten.

Gezielte Realitätsverzerrungen

Auch der schnellste Weg kann mit Hilfe von Kürzeste-Wege-Algorithmen berechnet werden. Dafür verwendet man anstatt der Länge (z.B. in Kilometern) die Zeit (z.B. in Stunden oder Minuten), die man voraussichtlich für die Straße (Kante) braucht. Man rechnet also Länge (s) geteilt durch erwartete Geschwindigkeit (v) für jede Kante des Graphen.

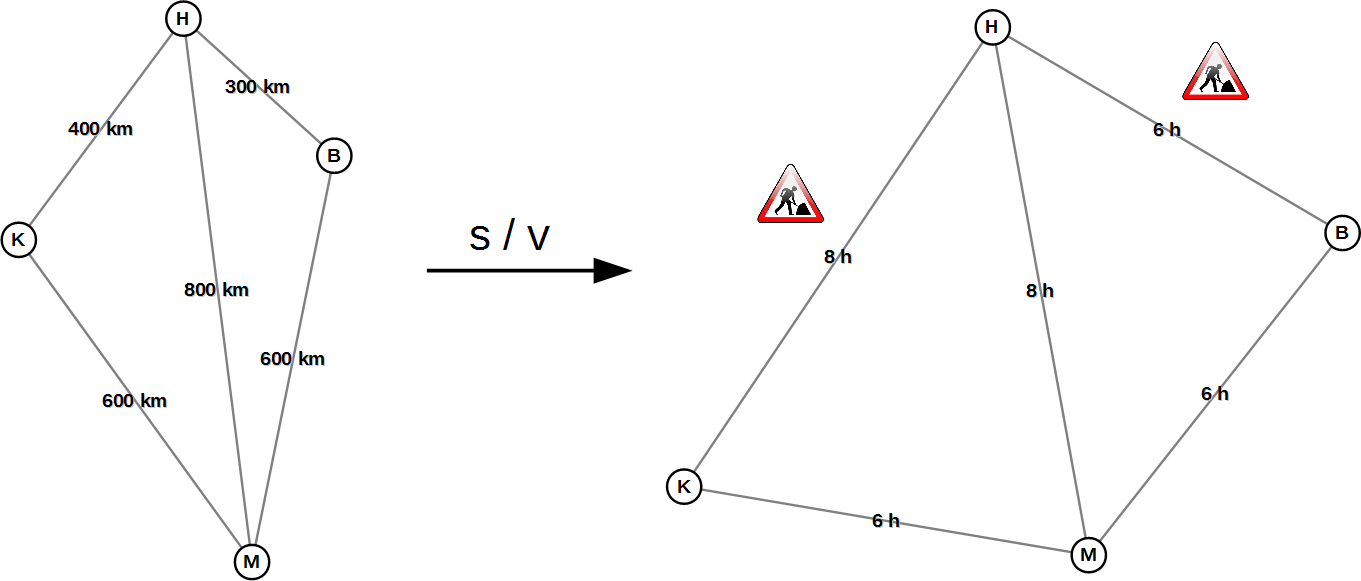
veloc-viz

Abb. 1: Die Städte Hamburg (H), Berlin (B), Köln (K) und München (M). Links ein Graph mit den zu fahrenden Kilometern, rechts ein Graph mit den benötigten Fahrzeiten.

In Abbildung 1 ist ein Beispiel zu sehen, wie ein Graph transformiert wird, wenn man die benötigte Zeit berücksichtigt. Wir nehmen hier an, dass man zwischen den Städten Hamburg, Berlin, Köln und München immer 100 km/h fahren kann, außer auf den Strecken Köln-Hamburg und Hamburg-Berlin, wo auf Grund von Bauarbeiten nur 50 km/h möglich sind. Das Ergebnis ist, dass Hamburg deutlich weiter von Berlin und Köln „wegrückt“ und der schnellste Weg von Köln nach Berlin jetzt über München führt. Der kürzeste Weg im transformierten Graphen (rechts) ist jetzt auch der schnellste Weg. Man kann daher auch den schnellsten Weg mit Hilfe eines Kürzeste-Wege-Algorithmus berechnen.

Ein ganz ähnlicher Trick führt bei der Suche nach dem zuverlässigsten Weg zum Erfolg. In Abbildung 2 ist ein fiktives Kommunikationsnetz zwischen einigen europäischen Ländern dargestellt. An den Kanten des Graphen steht jeweils eine Prozentangabe, die die Wahrscheinlichkeit ausdrückt, dass diese Kommunikationsverbindung funktioniert.

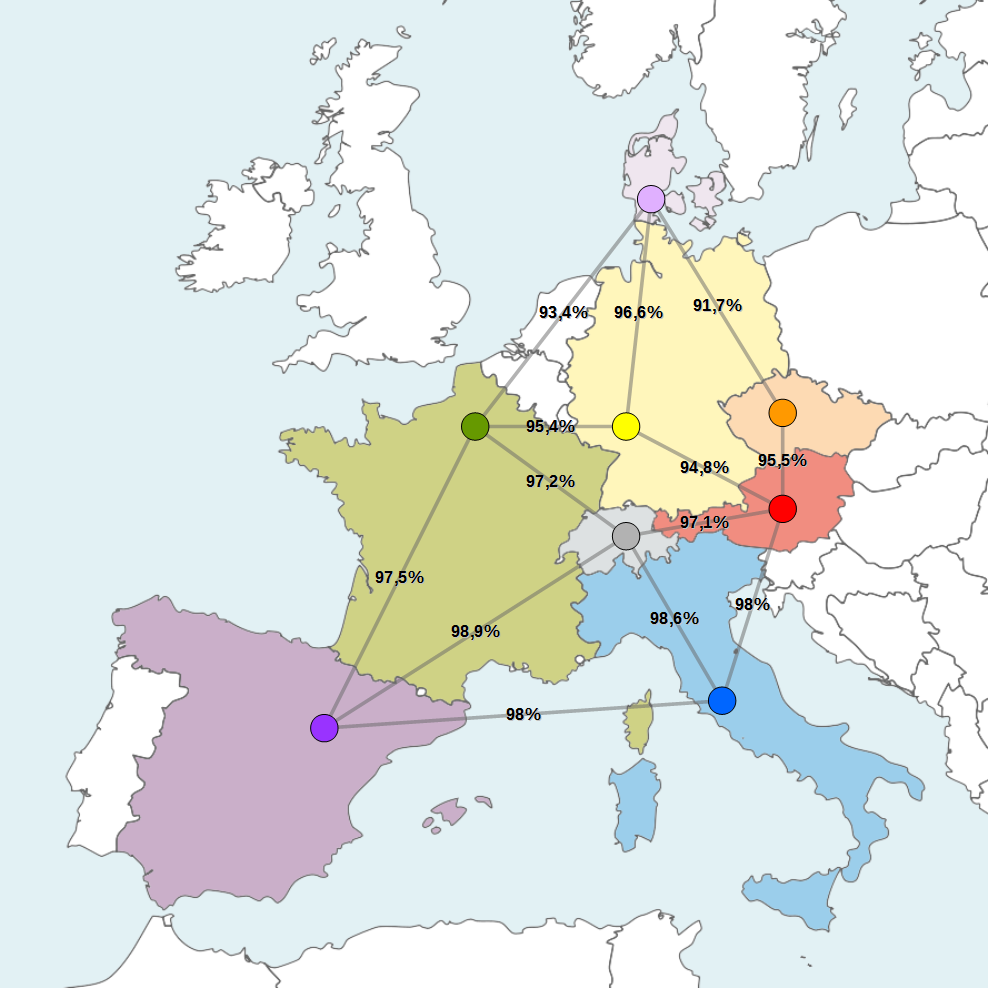
communications-network

Abb. 2: Fiktives Kommunikationsnetz zwischen einigen europäischen Ländern mit Angaben zur Zuverlässigkeit. Die Landkarte im Hintergrund basiert auf Blank map of Europe von W!B, Verwendung unter CC BY-SA 3.0

Um die Zuverlässigkeit eines Wegs zu berechnen, werden alle beteiligten Wahrscheinlichkeiten miteinander multipliziert. Die Zuverlässigkeit des Wegs von Italien (blau) nach Frankreich (grün) über die Schweiz (grau) liegt also bei 95,8392% (=0,986 · 0,972). Der zuverlässigste Weg von einem Startknoten zu einem Zielknoten ist derjenige, bei dem das Produkt der Wahrscheinlichkeiten maximal ist. Leider können Kürzeste-Wege-Algorithmen nur einen Weg finden, bei dem die Summe der Kantenlängen minimal ist. Die Algorithmen passen also nicht zu unserem Problem. Wir werden daher das Problem so modifizieren, dass es passt.

Der negative Logarithmus eilt zur Rettung

Zunächst interessieren wir uns natürlich nur für die Rohdaten. Das heißt, dass wir die Europakarte aus Abbildung 2 ignorieren können, da sie für Berechnungen nicht notwendig ist (siehe linker Graph in Abbildung 3). Jetzt wenden wir auf jede Prozentzahl den negativen Logarithmus an. Das bedeutet, wir ändern z.B. zwischen grün und gelb den Wert 0,954 (=95,4%) in -log(0,954). Der rechte Graph in Abbildung 3 zeigt das Ergebnis der Transformation. Die Werte des negativen Logarithmus werden dabei durch die Längen der Kanten visualisiert. Die Beschriftungen (Prozentangaben) sind der Übersichtlichkeit halber unverändert.

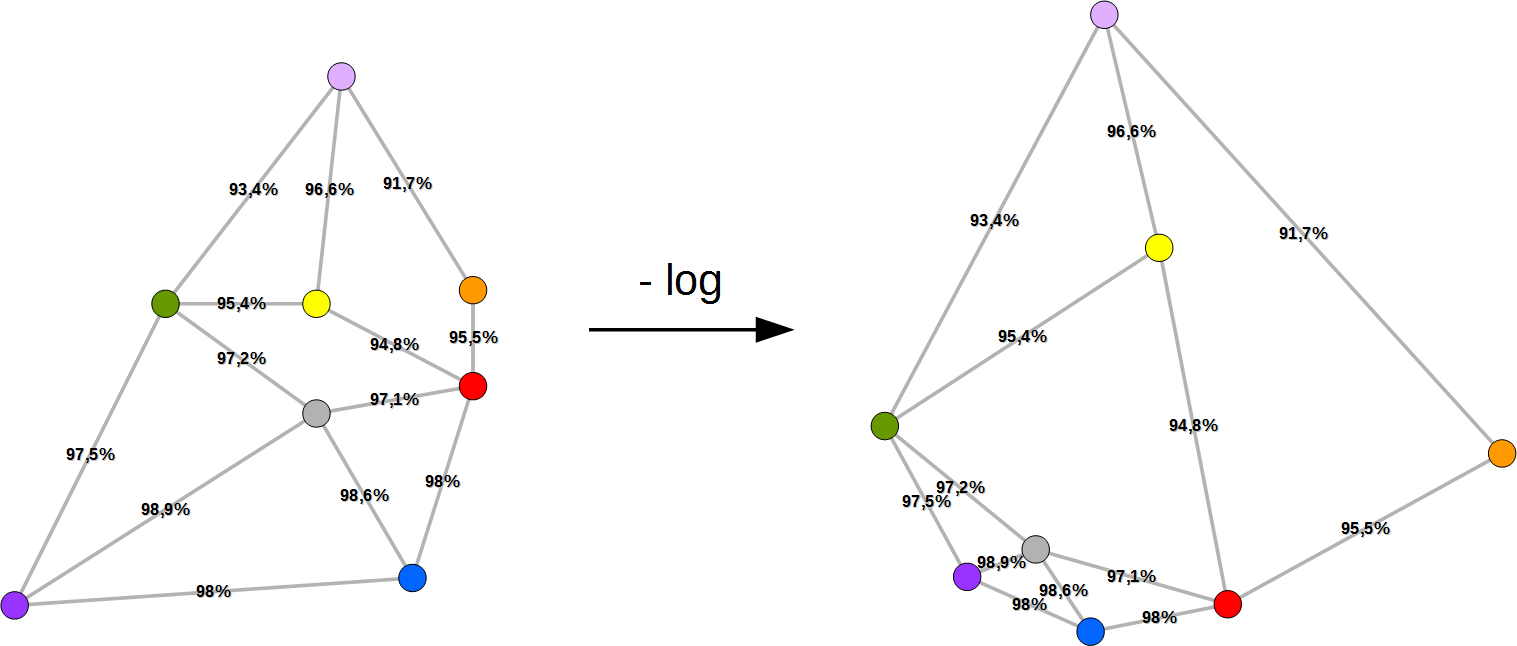
communications-network-transformation

Abb. 3: Graph des Kommunikationsnetzes vor und nach der Transformation mit dem negativen Logarithmus.

Erstaunlicherweise sind alle kürzesten Wege im transformierten Graphen (rechts) auch zuverlässigste Wege. Es ist daher auch leicht zu erkennen, dass z.B. der zuverlässigste Weg von Österreich (rot) nach Dänemark (hell-violett) durch Deutschland (gelb) führt oder, dass der zuverlässigste Weg von Österreich (rot) nach Frankreich (grün) über die Schweiz (grau) geht. So funktioniert die Reduktion des Problems des zuverlässigsten Wegs auf das Problem des kürzesten Wegs. Ziemlich cool, oder?

Ich habe diesen Trick nicht selbst entdeckt. Er ist schon mindestens seit 1975 bekannt (siehe [1] und [2]). Vermutlich gab es damals aber nicht so schöne bunte Bilder zur Veranschaulichung. 🙂

Warum es funktioniert

Um zu zeigen, warum die Transformation mit dem negativen Logarithmus den beschriebenen Nutzen hat, müssen wir unser Problem mathematisch betrachten. Es folgt also jetzt eine mathematische Formulierung des zuverlässigsten Wegs und eine schrittweise Umformung, wobei jeder Schritt erklärt wird:

(1)   \begin{equation*} \newcommand{\argmax}{\operatornamewithlimits{argmax}} \argmax_p \prod_{p_i \in p} p_i = ... \end{equation*}

(1) Der erste Term drückt aus, dass wir den Weg p suchen, sodass das Produkt der Wahrscheinlichkeiten pi des Wegs p maximal ist. Die Funktion argmax drückt dabei aus, dass uns nicht der Wert der maximalen Zuverlässigeit interessiert (in diesem Fall müsste es max heißen), sondern der Weg p, bei dem dieser Wert erreicht wird. Ein kleiner aber feiner Unterschied.

(2)   \begin{equation*} \newcommand{\argmax}{\operatornamewithlimits{argmax}} \argmax_p ( \log \prod_{p_i \in p} p_i) = ... \end{equation*}

(2) Da der Logarithmus eine streng monoton steigende Funktion ist, können wir ihn anwenden, ohne dass sich die Lösung der Maximierungsaufgabe verändert.

(3)   \begin{equation*} \newcommand{\argmax}{\operatornamewithlimits{argmax}} \argmax_p \sum_{p_i \in p} \log p_i = ... \end{equation*}

(3) Der Logarithmus des Produkts ist gleich der Summe der Logarithmen. Das ist eine sehr praktische Eigenschaft des Logarithmus. Gleich haben wir es geschafft!

(4)   \begin{equation*} \newcommand{\argmin}{\operatornamewithlimits{argmin}} \argmin_p ( - \sum_{p_i \in p} \log p_i) = ... \end{equation*}

(4) Anstatt das Maximum für die Summe zu suchen, können wir auch ein Minuszeichen vor die Summe schreiben und von nun an nach dem Minimum suchen.

(5)   \begin{equation*} \newcommand{\argmin}{\operatornamewithlimits{argmin}} \argmin_p \sum_{p_i \in p} -\log p_i \end{equation*}

(5) Anstatt die ganze Summe zu negieren, kann man auch die einzelnen Summanden negieren. Was bedeutet dieser Term? Wir suchen Jetzt nach einem Weg, für den die Summe der Längen der Wege (jeweils -log pi) minimal ist, was wieder dem Kürzeste-Wege-Problem entspricht.

Fazit

Das Problem des zuverlässigsten Wegs kann mit Hilfe eines beliebigen Kürzeste-Wege-Algorithmus gelöst werden. Man muss nur auf die Wahrscheinlichkeit jeder Kante des Graphen den negativen Logarithmus anwenden und die Ergebnisse als Längen für den Kürzeste-Wege-Algorithmus verwenden.

Literatur

  1. CHRISTOFIDES, Nicos. Graph Theory – An Algorithmic Approach. New York: Academic Press Inc, 1975.
  2. ROOSTA, Mohammad. Routing through a network with maximum reliability. Journal of Mathematical Analysis and Applications, 1982, 88. Jg., Nr. 2, S. 341-347.
    M Roosta, J. Math. Anal. Appl., 88 (1982), pp. 341–347

Ähnliche Artikel

3 Gedanken zu „Problemreduktion – Der sicherste Weg ist auch nur ein kürzester Weg“

  2. Brunner Josef B.

    Interessant wird das Problem, wenn man es mit Excel VAP löst. 1. Tabelle: = Knotenpunkte
    2. Tabelle = Vektoren, Visierlinie. gesperrte Strecken auf Hin und Rückweg, Zeiten
    3. Tabelle = Verbindungen zwischen den Knoten
    4. Tabelle = grafische Darstellung von Knoten und Vektoren plus Markierung der resultierenden Strecken
    Auf Blatt 0 sind Azsgangangspunkt und Ziel, Zeiten in Minuten für Distanzen und Höhendifferenzen angegeben.

    Antworten ↓

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert