Kaum ein Thema kann einen Studienanfänger so vor den Kopf stoßen wie diese seltsamen „Algebraischen Strukturen“ aus der Mathematik-Vorlesung. Eigentlich ist man doch angetreten, um reale Probleme zu lösen und jetzt erklärt einem dieser Professor mit ernster Miene, dass es so etwas wie Addition und Multiplikation tatsächlich gibt und das erstaunlicherweise 0 ungleich 1 ist. Was hat das denn mit der realen Welt zu tun?

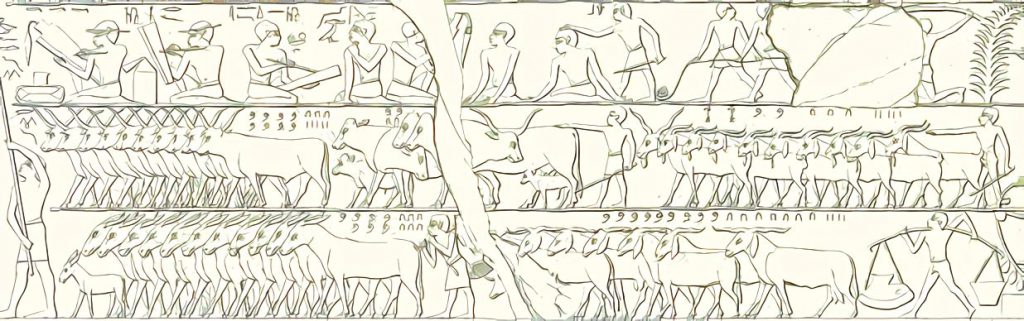
Seit Jahrtausenden hat es sich bewährt, Dinge (z.B. Ziegen) zu zählen und das Ergebnis als Zahl zu notieren. Diese aufgeschriebenen Zahlen werden dann häufig zusammengezählt (d.h. addiert), um die Gesamtzahl aller Dinge ohne nochmaliges Zählen zu bestimmen. Selbst die alten Ägypter konnten bereits berechnen, dass es in Abbildung 1 um insgesamt 3209 (=2235+974) Ziegen geht.

Manchmal ist auch das Vielfache einer Zahl interessant (z.B. „Wenn auf ein Schiff 20 Krieger passen, dann passen auf 7 Schiffe?“), was man Multiplikation nennt. Addition und Multiplikation müssen manchmal auch umgekehrt werden (Subtraktion und Division). Soweit so gut. Aber eigentlich haben wir das alles bereits in der Grundschule gelernt.

Objekte für mathematische Operationen

Zahlen sind Objekte, auf denen man mathematische Operationen durchführen kann. Addition, Subtraktion, Multiplikation und Division sind Beispiele dafür, aber es gibt auch komplexere Operationen und Objekte.

Ein Beispiel hierfür ist die Bestimmung des größten gemeinsamen Teilers. Der euklidische Algorithmus, der diesen bestimmt, kann auf ganze Zahlen ausgeführt werden. Die Verwendung anderer mathematischer Objekte, wie z.B. Polynome, ist aber möglich, solange es eine Division mit Rest gibt. Man nennt derartige mathematische Objekte Euklidische Ringe.

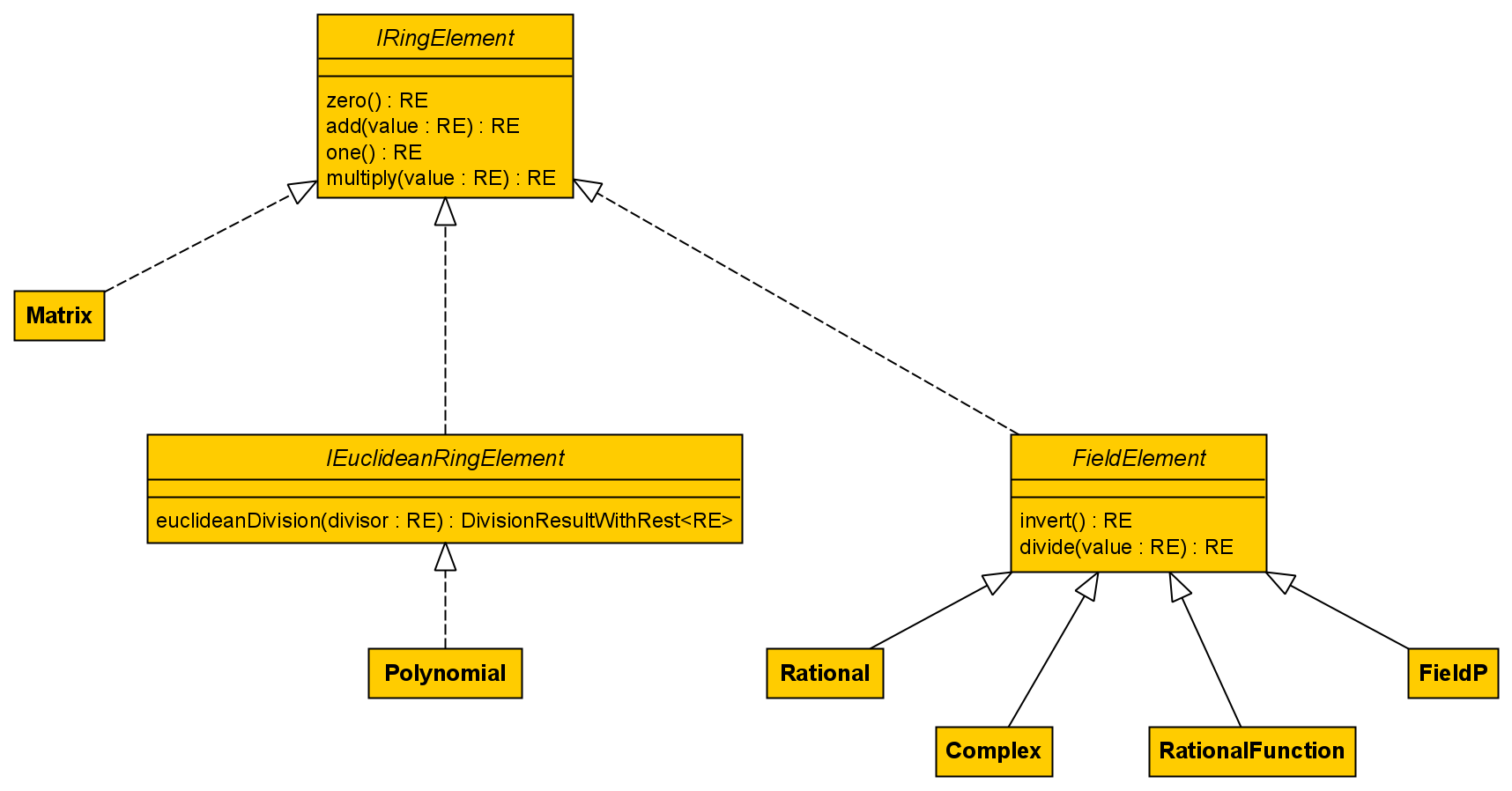
In Abbildung 2 sind einige Algebraische Strukturen als Klassendiagramm dargestellt, wie sie in JLinAlg – einer in Java implementierten Open-Source-Bibliothek zur Linearen Algebra – verwendet werden. Auch in JLinAlg gibt es eine Implementierung des Euklidischen Algorithmus, die auf Objekte angewendet werden kann, die das Interface IEuclideanRingElement implementieren. Der Euklidische Algorithmus funktioniert also analog zu ganzen Zahlen auch bei Polynomen (Klasse Polynomial), aber nicht bei Objekten vom Typ Matrix und im Allgemeinen auch nicht für Körper (d.h. Unterklassen von FieldElement).

Worum es wirklich geht

Genauso wie die meisten Menschen Äpfel addieren können wie Birnen, sollte ein Student in den MINT-Fächern (d.h. in den Fächern Mathematik, Informatik, Naturwissenschaften und Technik) lernen, alles Mögliche miteinander verknüpfen zu können:

• Verbindungen aus Fahrplänen, Straßen- oder Kommunikationsnetzen
• Elektronische Schaltkreise
• Private und öffentliche Schlüssel beim Signieren und Verschlüsseln von Daten
• Bedienelemente wie Text-Eingabefelder und Knöpfe
• Arbeitsschritte bei der Prozessoptimierung
• Objekte in Programmiersprachen

Dabei handelt es sich natürlich oft nicht mehr um algebraische Strukturen, aber die Grundidee ist immer die gleiche. Für all diese Verknüpfungen/Algorithmen gelten Bedingungen und wenn die Eigenschaften der zugrundeliegenden Strukturen ähnlich genug sind, können Verfahren, die bei einem Problem angewendet werden können, auch bei einem anderen zum Einsatz kommen. So kann man z.B. einen kürzesten Weg sowohl in einem Straßennetz als auch mit Hilfe eines Fahrplans finden.

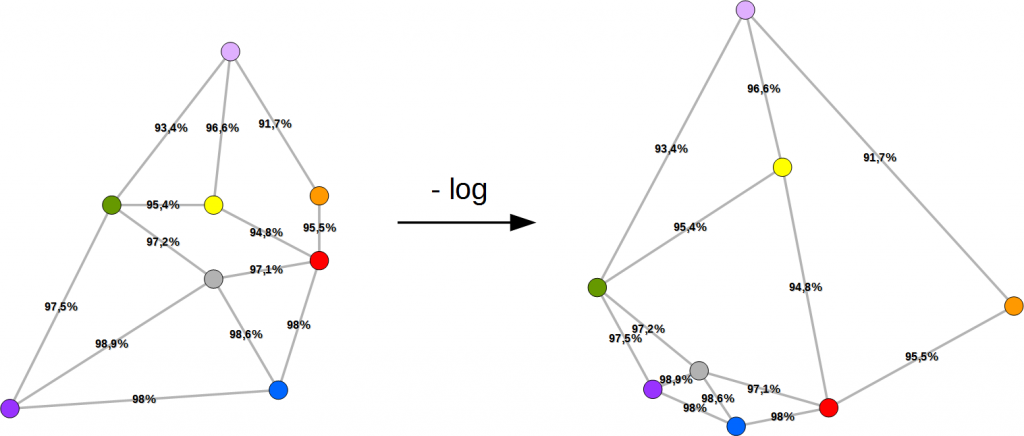
Bei vielen Problemen muss man etwas nachhelfen, damit ein altbekanntes Verfahren zur Lösung eines neuen Problems führt. Dies kann z.B. mit Hilfe einer mathematischen Transformation der Problemstellung erreicht werden, wie im Artikel Problemreduktion – Der sicherste Weg ist auch nur ein kürzester Weg beschrieben (siehe auch Abbildung 3).

Appell an alle MINT-Studenten

Mir ist klar, dass es schwierig ist, sich für Vorlesungen wie Lineare Algebra, Analysis oder Stochastik zu motivieren. Eure Gehirne sollen dabei ein Stück weit umkonfiguriert werden – und das kann schmerzhaft sein. Manchmal ist es aber auch ziemlich cool, was man seinem Gehirn alles beibringen kann.

Die Denkweisen, die ihr lernt, sind abstrakt – bisweilen auch recht praxisfern, doch je mehr ihr darüber wisst und im Kopf behaltet (!), desto weniger stümperhaft werden eure Lösungsansätze sein, die ihr im Arbeitsleben verfolgt. Durchhalten! Es lohnt sich.